Formulácia problému

Zadanie predpokladá, že používateľ je oboznámený so základnými pojmami numerických metód, ako sú determinantná a inverzná matica, a rôzne cesty ich výpočty. V tejto teoretickej správe sú v jednoduchom a prístupnom jazyku najskôr predstavené základné pojmy a definície, na základe ktorých prebieha ďalší výskum. Užívateľ nemusí mať špeciálne znalosti v oblasti numerických metód a lineárnej algebry, ale môže ľahko využiť výsledky tejto práce. Pre prehľadnosť je predstavený program na výpočet determinantu matice niekoľkými metódami, napísaný v programovacom jazyku C ++. Program sa používa ako laboratórna lavica na vytváranie ilustrácií k správe. Vykonáva sa tiež výskum metód na riešenie systémov lineárnych algebraických rovníc. Užitočnosť výpočtu inverznej matice je dokázaná, preto práca poskytuje optimálnejšie metódy na riešenie rovníc bez jej výpočtu. Tento článok vysvetľuje, prečo existuje toľko rôznych metód na výpočet determinantov a inverzných matíc, a rozoberá ich nevýhody. Tiež sa berú do úvahy chyby pri výpočte determinantu a odhaduje sa dosiahnutá presnosť. Okrem ruských výrazov práca používa aj ich anglické ekvivalenty, aby pochopila, pod akými názvami hľadať numerické postupy v knižniciach a čo znamenajú ich parametre.

Základné definície a najjednoduchšie vlastnosti

Determinant

Predstavme definíciu determinantu štvorcovej matice akéhokoľvek poradia. Táto definícia bude opakujúci to znamená, že na zistenie toho, čo je determinantom matice rádu, musí už človek vedieť, čo je determinantom matice rádu. Všimnite si tiež, že determinant existuje iba pre štvorcové matice.

Determinant štvorcovej matice bude označený alebo det.

Definícia 1. Determinantštvorcová matica druhá objednávka je číslo .

Determinant štvorcová matica poriadku sa nazýva číslo

kde je determinant matice poradia získanej z matice odstránením prvého riadka a stĺpca s číslom.

Pre prehľadnosť zapisujeme, ako môžete vypočítať determinant matice štvrtého rádu:

Komentovať. Skutočný výpočet determinantov pre matice vyššieho rádu troch na základe definície sa používa vo výnimočných prípadoch. Výpočet sa spravidla vykonáva podľa iných algoritmov, o ktorých sa bude diskutovať neskôr a ktoré vyžadujú menej výpočtovej práce.

Komentovať. V definícii 1 by bolo presnejšie povedať, že determinant je funkcia definovaná na súbore štvorcových matíc rádu a nadobúdajúca hodnoty v množine čísel.

Komentovať. V literatúre sa namiesto pojmu „determinant“ používa aj výraz „determinant“, ktorý má rovnaký význam. Od slova „determinant“ vyplynulo označenie det.

Uvažujme o niektorých vlastnostiach determinantov, ktoré formulujeme vo forme vyhlásení.

Vyhlásenie 1. Keď je matica transponovaná, determinant sa nemení, to znamená.

Vyhlásenie 2. Determinant súčinu štvorcových matíc sa rovná súčinu determinantov faktorov, tj.

Vyhlásenie 3. Ak sú dva riadky zamenené v matici, jeho determinant zmení znamienko.

Vyhlásenie 4. Ak má matica dva rovnaké riadky, jej determinant je nula.

V budúcnosti musíme pridať reťazce a reťazec vynásobiť číslom. Tieto operácie vykonáme na riadkoch (stĺpcoch) rovnakým spôsobom ako operácie na maticových radoch (maticových stĺpcoch), to znamená po elementoch. Výsledkom bude riadok (stĺpec), ktorý sa spravidla nezhoduje s riadkami pôvodnej matice. Ak existujú operácie na sčítanie riadkov (stĺpcov) a ich vynásobenie číslom, môžeme hovoriť aj o lineárnych kombináciách riadkov (stĺpcov), to znamená o súčtoch s číselnými koeficientmi.

Vyhlásenie 5. Ak je riadok matice vynásobený číslom, jeho determinant sa vynásobí týmto číslom.

Vyhlásenie 6. Ak matica obsahuje nulový riadok, jej determinant je nula.

Vyhlásenie 7. Ak je jeden z riadkov matice rovnaký ako druhý vynásobený číslom (riadky sú proporcionálne), potom je determinant matice nula.

Vyhlásenie 8. Nech i-tý riadok v matici má tvar. Potom, kde je matica získaná z matice nahradením i-teho riadku riadkom a matica-nahradením i-tého riadka riadkom.

Vyhlásenie 9. Ak do jedného z riadkov matice pridáte ďalší, vynásobený číslom, potom sa determinant matice nezmení.

Vyhlásenie 10. Ak je jeden z riadkov matice lineárnou kombináciou ostatných riadkov, potom je determinant matice nula.

Definícia 2. Algebraický doplnok k maticovému prvku je číslo rovné, kde je determinant matice získaný z matice odstránením i-tého riadka a j-týho stĺpca. Označí sa algebraický doplnok maticového prvku.

Príklad. Nechaj byť ... Potom

Komentovať. Použitím algebraických doplnkov možno definíciu 1 determinantu napísať nasledovne:

Vyhlásenie 11. Rozklad determinantu na ľubovoľnom reťazci.

Determinant matice vyhovuje vzorcu

Príklad. Vypočítajte .

Riešenie. Použime rozklad na treťom riadku, je to výnosnejšie, pretože v treťom riadku sú dve z troch čísel nuly. Dostaneme

Vyhlásenie 12. Pre štvorcovú maticu poriadku v platí nasledujúci vzťah: .

Vyhlásenie 13. Všetky vlastnosti determinantu formulovaného pre riadky (výroky 1 - 11) platia aj pre stĺpce, platí najmä rozklad determinantu v j -tom stĺpci a rovnosť o.

Vyhlásenie 14. Determinant trojuholníkovej matice sa rovná súčinu prvkov jej hlavnej uhlopriečky.

Dôsledok. Determinant matice identity je rovný jednej ,.

Výkon. Vyššie uvedené vlastnosti umožňujú nájsť determinanty matíc dostatočne vysokých rádov s relatívne malým počtom výpočtov. Algoritmus výpočtu je nasledujúci.

Algoritmus na vytváranie núl v stĺpci. Nech je požadovaný výpočet determinantu objednávky. Ak, potom vymeníme prvý riadok a všetky ostatné, v ktorých prvý prvok nie je nula. Výsledkom bude, že determinant sa bude rovnať determinantu novej matice s opačným znamienkom. Ak je prvý prvok v každom riadku rovný nule, potom má matica nulový stĺpec a podľa tvrdení 1, 13 je jeho determinant rovný nule.

Považujeme to teda už za pôvodnú maticu. Nechajte prvý riadok nezmenený. Pridajte do druhého riadku prvý riadok vynásobený číslom. Potom bude prvý prvok druhého radu .

Ostatné prvky nového druhého riadku budú označené symbolom. Determinant novej matice podľa vyhlásenia 9 je. Prvý riadok sa vynásobí číslom a pridá sa k tretiemu. Prvým prvkom nového tretieho riadku bude

Ostatné prvky nového tretieho riadku budú označené symbolom. Determinant novej matice podľa vyhlásenia 9 je.

Budeme pokračovať v procese získavania núl namiesto prvých prvkov riadkov. Nakoniec sa prvý riadok vynásobí číslom a pridá sa k posledný riadok... V dôsledku toho sa získa matica, ktorú označíme a ktorá má tvar

navyše. Na výpočet determinantu matice použijeme expanziu v prvom stĺpci

Odvtedy

Determinant matice poradia je na pravej strane. Použije sa naň rovnaký algoritmus a výpočet determinantu matice sa zredukuje na výpočet determinantu matice poradia. Proces opakujeme, kým nedosiahneme determinant druhého rádu, ktorý sa vypočíta podľa definície.

Ak matica nemá žiadne špecifické vlastnosti, potom nie je možné výrazne znížiť množstvo výpočtov v porovnaní s navrhovaným algoritmom. Ďalšou dobrou stránkou tohto algoritmu je, že je ľahké ho použiť na zostavenie počítačového programu na výpočet determinantov matíc veľkých rádov. V. štandardné programy pri výpočte determinantov sa tento algoritmus používa s menšími zmenami spojenými s minimalizáciou účinku chýb zaokrúhľovania a chýb vstupných údajov pri počítačových výpočtoch.

Príklad. Vypočítajte determinant matice .

Riešenie. Nechajte prvý riadok nezmenený. Do druhého riadku pridáme prvý vynásobený číslom:

Determinant sa nemení. Do tretieho riadku pridáme prvý vynásobený číslom:

Determinant sa nemení. Do štvrtého riadka pridajte prvý vynásobený číslom:

Determinant sa nemení. Výsledkom je, že dostaneme

Pomocou rovnakého algoritmu vypočítame determinant matice rádu 3 vpravo. Prvý riadok necháme nezmenený, do druhého riadku pridáme prvý vynásobený číslom :

Do tretieho riadku pridáme prvý vynásobený číslom :

Výsledkom je, že dostaneme

Odpoveď. .

Komentovať. Aj keď boli pri výpočtoch použité zlomky, výsledkom bolo celé číslo. Použitím vlastností determinantov a skutočnosti, že počiatočné čísla sú celé čísla, sa operácii so zlomkami dalo vyhnúť. Ale v inžinierskej praxi sú čísla len zriedka celé. Prvkami determinantu budú preto spravidla desatinné zlomky a nie je praktické použiť niektoré triky na zjednodušenie výpočtov.

inverzná matica

Definícia 3. Matica sa nazýva inverzná matica pre štvorcovú maticu, ak.

Z definície vyplýva, že inverznou maticou bude štvorcová matica rovnakého poradia ako matica (inak jeden z produktov alebo by nebol definovaný).

Inverzná matica pre maticu je označená. Ak teda existuje, potom.

Z definície inverznej matice vyplýva, že matica je inverznou maticou, to znamená. O matriciach a môžeme povedať, že sú navzájom inverzné alebo navzájom inverzné.

Ak je determinant matice nula, potom jej inverzná hodnota neexistuje.

Pretože je dôležité nájsť inverznú maticu, či je determinant Maritsy rovný nule alebo nie, uvádzame nasledujúce definície.

Definícia 4. Nazýva sa štvorcová matica degenerovať alebo špeciálna matica, ak nedegenerovaný alebo nesingulárna matica, ak.

Vyhlásenie. Ak inverzná matica existuje, je jedinečná.

Vyhlásenie. Ak je štvorcová matica nedegenerovaná, potom existuje jej inverzná a (1) kde sú algebraické doplnky k prvkom.

Veta. Inverzná matica pre štvorcovú maticu existuje vtedy a len vtedy, ak je matica nedegenerovaná, inverzná matica je jedinečná a platí vzorec (1).

Komentovať. Osobitnú pozornosť treba venovať miestam obsadeným algebraickými adíciami vo vzorci inverznej matice: prvý index ukazuje číslo stĺpci a druhé je číslo struny, do ktorého musíte napísať vypočítaný algebraický doplnok.

Príklad. .

Riešenie. Nájdite determinant

Pretože matica nie je zdegenerovaná a existuje jej inverzia. Nájdite algebraické doplnky:

Zostavíme inverznú maticu a nájdené algebraické doplnky umiestnime tak, aby prvý index zodpovedal stĺpcu a druhý do riadka: (2)

Výsledná matica (2) je odpoveďou na problém.

Komentovať. V predchádzajúcom prípade by bolo presnejšie napísať odpoveď takto:
(3)

Zápis (2) je však kompaktnejší a je vhodnejšie vykonať s ním ďalšie výpočty, ak sú potrebné. Preto je vhodnejšie napísať odpoveď vo forme (2), ak sú prvky matíc celé čísla. Naopak, ak sú prvkami matice desatinné zlomky, potom je lepšie napísať inverznú maticu bez činiteľa vpredu.

Komentovať. Pri hľadaní inverznej matice musíte vykonať pomerne veľa výpočtov a neobvyklé pravidlo na usporiadanie algebraických doplnkov v konečnej matici. Preto existuje vysoká pravdepodobnosť chyby. Aby ste sa vyhli chybám, mali by ste vykonať kontrolu: vypočítajte súčin pôvodnej a konečnej matice v jednom alebo inom poradí. Ak je výsledkom matica identity, inverzná hodnota sa nájde správne. V opačnom prípade musíte hľadať chybu.

Príklad. Nájdite inverznú hodnotu matice .

Riešenie. - existuje.

Odpoveď: .

Výkon. Nájdenie inverznej matice pomocou vzorca (1) vyžaduje príliš veľa výpočtov. To je neprijateľné pre matice štvrtého rádu a vyššie. Skutočný algoritmus na nájdenie inverznej matice bude uvedený neskôr.

Výpočet determinantnej a inverznej matice pomocou Gaussovej metódy

Na nájdenie determinantu a inverznej hodnoty matice je možné použiť Gaussovu metódu.

Totiž determinant matice sa rovná det.

Inverznú maticu nájdeme riešením systémov lineárnych rovníc pomocou Gaussovej eliminačnej metódy:

Kde je j-tý stĺpec matice identity, je požadovaný vektor.

Získané vektory roztoku - zrejme tvoria stĺpce matice, pretože.

Determinantné vzorce

1. Ak matica nie je generovaná, potom a (súčin otočných prvkov).

V priebehu riešenia úloh vo vyššej matematike je to veľmi často nevyhnutné vypočítajte determinant matice... Determinant matice sa vyskytuje v lineárnej algebre, analytickej geometrii, matematickej analýze a ďalších odvetviach vyššej matematiky. Človek sa teda jednoducho nezaobíde bez schopnosti riešiť determinanty. Aj pre vlastné testovanie si môžete zadarmo stiahnuť kalkulačku determinantov, ktorá vás sama o sebe nenaučí, ako riešiť determinanty, ale je to veľmi praktické, pretože je vždy dobré poznať správnu odpoveď vopred!

Nebudem uvádzať presnú matematickú definíciu determinantu a vo všeobecnosti sa pokúsim minimalizovať matematickú terminológiu, väčšina čitateľov to nebude mať jednoduchšie. Cieľom tohto článku je naučiť vás riešiť determinanty druhého, tretieho a štvrtého rádu. Všetok materiál je predložený jednoduchou a prístupnou formou a dokonca aj plná (prázdna) čajová kanvica vo vyššej matematike po starostlivom preštudovaní materiálu bude schopná správne vyriešiť determinanty.

V praxi najčastejšie nájdete determinant druhého rádu, napríklad :, a determinant tretieho rádu, napríklad: .

Determinant štvrtého rádu tiež nie starožitnosti, a na to prídeme na konci hodiny.

Dúfam, že každý rozumie nasledujúcemu:Čísla vo vnútri determinantu žijú samy o sebe a o žiadnom odpočítaní nemôže byť ani reč! Nemôžete zamieňať čísla!

(Konkrétne je možné vykonávať spárované permutácie riadkov alebo stĺpcov determinantu so zmenou jeho znamienka, ale často to nie je potrebné - pozrite si nasledujúcu lekciu Vlastnosti determinantu a zníženie jeho poradia)

Ak je teda daný nejaký determinant, potom v jeho vnútri sa ničoho nedotýkajte!

Označenia: Ak je daná matica , potom sa označí jeho determinant. Determinant je tiež veľmi často označovaný latinským písmenom alebo gréčtinou.

1)Čo to znamená vyriešiť (nájsť, odhaliť) determinant? Výpočet determinantu znamená ZISTENIE ČÍSLA. Otázniky vo vyššie uvedených príkladoch sú úplne bežné čísla.

2) Teraz zostáva prísť na to AKO NÁJSŤ TOTO ČÍSLO? Na to musíte použiť určité pravidlá, vzorce a algoritmy, o ktorých sa teraz bude diskutovať.

Začnime kvalifikáciou „dva“ až „dva“:

TOTO BY SI MAL PAMATOVAŤ, prinajmenšom počas štúdia vyššej matematiky na univerzite.

Hneď sa pozrime na príklad:

Pripravený. Najdôležitejšou vecou je NEZMIENAŤ SA V ZNAČKÁCH.

Determinant matice tri krát tri dajú sa otvoriť 8 spôsobmi, z toho 2 sú jednoduché a 6 bežných.

Začnime dvoma jednoduché spôsoby

Podobne ako v kvalifikátore „dva po dvoch“, aj kvalifikátor „tri po troch“ je možné rozšíriť podľa vzorca:

Vzorec je dlhý a nepozornosťou je ľahké urobiť chybu. Ako sa vyhnúť nepríjemným chybám? Na tento účel bol vynájdený druhý spôsob výpočtu determinantu, ktorý sa v skutočnosti zhoduje s prvým. Hovorí sa mu Sarrusova metóda alebo metóda „rovnobežných pruhov“.
Spodný riadok je ten, že napravo od determinantu sú priradené prvý a druhý stĺpec a čiary sú úhľadne nakreslené ceruzkou:

Multiplikátory na „červených“ uhlopriečkach sú zahrnuté vo vzorci so znamienkom „plus“.
Faktory na „modrých“ uhlopriečkach sú zahrnuté vo vzorci so znamienkom mínus:

Príklad:

Porovnajte tieto dve riešenia. Je ľahké vidieť, že je to JEDNO A TÉŽ, len v druhom prípade sú multiplikátory vzorca mierne preskupené a čo je najdôležitejšie, pravdepodobnosť chyby je oveľa menšia.

Teraz sa pozrime na šesť bežných spôsobov výpočtu determinantu

Prečo normálne? Pretože v drvivej väčšine prípadov je potrebné týmto spôsobom odhaliť kvalifikátorov.

Ako vidíte, kvalifikátor tri na tri má tri stĺpce a tri riadky.
Determinant je možné vyriešiť jeho rozšírením v ktoromkoľvek riadku alebo stĺpci.
Získa sa teda 6 spôsobov, pričom sa vo všetkých prípadoch používa rovnakého typu algoritmus.

Determinant matice sa rovná súčtu súčinov prvkov riadka (stĺpca) zodpovedajúcimi algebraickými doplnkami. Bojazlivo? Všetko je oveľa jednoduchšie, použijeme nevedecký, ale zrozumiteľný prístup, prístupný aj osobe ďaleko od matematiky.

V nasledujúcom príklade rozbalíme determinant na prvom riadku.
Na to potrebujeme maticu znakov:. Je ľahké vidieť, že značky sú rozložené.

Pozor! Matica znakov je môj vlastný vynález. Tento koncept nie je vedecký, nemusí byť použitý pri konečnom návrhu úloh, iba vám pomôže porozumieť algoritmu na výpočet determinantu.

Najprv vám poskytnem úplné riešenie. Opäť vezmeme náš experimentálny determinant a vykonáme výpočty:

A hlavná otázka: AKO to získať z kvalifikácie „tri po troch“:
?

Determinant „tri krát tri“ sa teda redukuje na riešenie troch malých determinantov, alebo ako sa im tiež hovorí, MINOROV... Odporúčam zapamätať si tento výraz, najmä preto, že je zapamätateľný: maloletý je malý.

Pretože je zvolený spôsob rozkladu determinantu na prvom riadku Je zrejmé, že sa všetko točí okolo nej:

Položky sa zvyčajne zobrazujú zľava doprava (alebo zhora nadol, ak bol vybratý stĺpec)

Poďme, najskôr sa zaoberáme prvým prvkom riadku, to znamená s jednotkou:

1) Z matice znakov vypíšeme zodpovedajúce znamienko:

2) Potom napíšeme samotný prvok:

3) DOMÁCNE preškrtnite riadok a stĺpec, v ktorom sa nachádza prvý prvok:

Zostávajúce štyri čísla tvoria determinant „dva po dvoch“, ktorý sa nazýva MINOROM tohto prvku (jednotky).

Prejdeme k druhému prvku riadku.

4) Z matice znakov vypíšeme zodpovedajúce znamienko:

5) Potom napíšeme druhý prvok:

6) MYSLITE SI preškrtnite riadok a stĺpec, v ktorom je umiestnený druhý prvok:

Tretí prvok prvého riadku. Žiadna originalita:

7) Z matice znakov vypíšeme zodpovedajúce znamienko:

8) Zapíšeme tretí prvok:

9) DOMÁCNE preškrtnite riadok a stĺpec, ktorý obsahuje tretí prvok:

Zostávajúce štyri čísla napíšeme na malý determinant.

Ostatné akcie nie sú ťažké, pretože už vieme, ako počítať determinanty dva po dvoch. Nenechajte sa zmiasť znakmi!

Podobne môže byť determinant rozbalený v ľubovoľnom riadku alebo stĺpci. Prirodzene, vo všetkých šiestich prípadoch je odpoveď rovnaká.

Determinant štyrikrát štyri možno vypočítať pomocou rovnakého algoritmu.
V tomto prípade sa matica znakov zvýši:

V nasledujúcom príklade som rozšíril kvalifikátor vo štvrtom stĺpci:

A ako sa to stalo, skúste na to prísť sami. Ďalšie informácie Bude neskôr. Ak chce niekto vyriešiť determinant do konca, správna odpoveď je: 18. Pre prax je lepšie otvoriť determinant nejakým iným stĺpcom alebo iným riadkom.

Cvičiť, odhaľovať a vykonávať výpočty je veľmi dobré a užitočné. Ale koľko času strávite veľkým determinantom? Nemohlo by to byť nejako rýchlejšie a spoľahlivejšie? Navrhujem, aby ste sa zoznámili s účinné metódy výpočet determinantov v druhej lekcii - Determinačné vlastnosti. Zníženie poradia determinantu.

BUĎ OPATRNÝ!

- Uvoľnite sýkorku na istú smrť!
Nechajte ju pohladiť slobodou!
A loď pláva a reaktor hučí ...
- Pash, si posratý?

Pamätám si, že pred 8. triedou som nemal rád algebru. Vôbec sa mi to nepáčilo. Nahnevala ma. Pretože som tam ničomu nerozumel.

A potom sa všetko zmenilo, pretože som prešiel jedným dielom:

V matematike všeobecne (a najmä v algebre) je všetko postavené na kompetentnom a konzistentnom systéme definícií. Poznáte definície, chápete ich podstatu - ostatné už nebude ľahké zistiť.

Tak je to aj s témou dnešnej hodiny. Podrobne zvážime niekoľko súvisiacich problémov a definícií, vďaka ktorým sa raz a navždy budete zaoberať maticami a determinantmi a všetkými ich vlastnosťami.

Determinanty sú ústredným pojmom v maticovej algebre. Rovnako ako skrátené vzorce násobenia vás budú prenasledovať počas celého kurzu matematiky pre pokročilých. Preto dôkladne čítame, sledujeme a rozumieme. :)

A začneme tým najintímnejším - a čo je matica? A ako s ním správne pracovať.

Správne usporiadanie indexov v matici

Matica je iba tabuľka naplnená číslami. Neo s tým nemá nič spoločné.

Jednou z kľúčových charakteristík matice je jej rozmer, t.j. počet riadkov a stĺpcov, z ktorých pozostáva. Obvykle hovoria, že nejaká matica $ A $ má veľkosť $ \ left [m \ times n \ right] $, ak má $ m $ riadkov a $ n $ stĺpcov. Píšu to takto:

Alebo takto:

Existujú aj iné označenia - všetko závisí od preferencií lektora / seminaristu / autora učebnice. Ale v každom prípade, so všetkými týmito $ \ left [m \ times n \ right] $ a $ ((a) _ (ij)) $, nastáva rovnaký problém:

Ktorý index je za čo zodpovedný? Najprv príde číslo riadku, potom stĺpec? Alebo naopak?

Pri čítaní prednášok a učebníc sa odpoveď bude zdať zrejmá. Ale keď máte pred sebou na skúške iba leták s problémom, môžete sa prepadnúť a zrazu sa zamotať.

Poďme sa teda raz a navždy zaoberať touto otázkou. Na začiatok si pripomeňme obvyklý súradnicový systém z kurzu školskej matematiky:

Predstavujeme súradnicový systém v rovine

Pamätáte si ju? Má pôvod (bod $ O = \ left (0; 0 \ right) $) osi $ x $ a $ y $ a každý bod v rovine je jednoznačne určený súradnicami: $ A = \ left (1; 2 \ vpravo) $, $ B = \ vľavo (3; 1 \ vpravo) $ atď.

Teraz vezmeme túto konštrukciu a umiestnime ju vedľa matice tak, aby pôvod bol v ľavom hornom rohu. Prečo tam? Pretože keď otvoríme knihu, začneme čítať presne z ľavého horného rohu stránky - je jednoduchšie si to zapamätať.

Kam by ale mali smerovať osi? Nasmerujeme ich tak, aby bola celá naša virtuálna „stránka“ pokrytá týmito osami. Je pravda, že na to musíte otočiť náš súradnicový systém. Jediná možná možnosť pre takéto usporiadanie:

Prekrytie súradnicového systému na matici

Teraz každá bunka matice má súradnice s jednou hodnotou $ x $ a $ y $. Napríklad písanie $ ((a) _ (24)) $ znamená, že máme na mysli prvok so súradnicami $ x = 2 $ a $ y = 4 $. Rozmery matice sú tiež jedinečne stanovené dvojicou čísel:

Definícia indexov v matici

Stačí sa pozorne pozrieť na tento obrázok. Hrajte sa so súradnicami (obzvlášť keď pracujete so skutočnými maticami a determinantami) - a veľmi skoro zistíte, že aj v tých najzložitejších vetách a definíciách dokonale rozumiete, o čo ide.

Rozumiete? Prejdeme k prvému kroku osvietenia - geometrickému vymedzeniu determinantu. :)

Geometrická definícia

Najprv by som rád poznamenal, že determinant existuje iba pre štvorcové matice tvaru $ \ left [n \ times n \ right] $. Determinant je číslo, ktoré sa vypočítava podľa určitých pravidiel a je jednou z charakteristík tejto matice (existujú aj ďalšie charakteristiky: hodnosť, vlastné vektory, ale o tom viac v iných hodinách).

Čo je teda táto vlastnosť? Čo to znamená? Je to jednoduché:

Determinant štvorcovej matice $ A = \ left [n \ times n \ right] $ je objem $ n $ -dimenzionálneho rovnobežnostena, ktorý vznikne, ak riadky matice považujeme za vektory tvoriace okraje tohto rovnobežnostenný.

Napríklad determinant matice 2x2 je len oblasť rovnobežníka a pre maticu 3x3 je to už objem trojrozmerného rovnobežnostenu - ten, ktorý rozhorčí všetkých stredoškolákov na hodinách stereometrie.

Na prvý pohľad sa táto definícia môže zdať úplne neadekvátna. Nerobme však unáhlené závery - pozrime sa na príklady. V skutočnosti je všetko elementárne, Watson:

Úloha. Nájdite determinanty matíc:

\ [\ vľavo | \ begin (matica) 1 & 0 \\ 0 & 3 \\\ end (matica) \ right | \ quad \ left | \ begin (matica) 1 & -1 \\ 2 & 2 \\\ end (matica) \ right | \ quad \ left | \ begin (matica) 2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\\ end (matica) \ right | \]

Riešenie. Prvé dve kvalifikácie sú 2x2. Preto sú to len oblasti rovnobežníkov. Nakreslíme ich a vypočítame plochu.

Prvý rovnobežník je postavený na vektoroch $ ((v) _ (1)) = \ left (1; 0 \ right) $ a $ ((v) _ (2)) = \ left (0; 3 \ right) $:

Determinant 2x2 je plocha rovnobežníka

Očividne to nie je len rovnobežník, ale celkom obdĺžnik. Jeho oblasť je

Druhý rovnobežník je postavený na vektoroch $ ((v) _ (1)) = \ left (1; -1 \ right) $ a $ ((v) _ (2)) = \ left (2; 2 \ right ) $. No a čo? Toto je tiež obdĺžnik:

Ďalší determinant 2x2

Strany tohto obdĺžnika (v skutočnosti dĺžky vektorov) sa dajú ľahko vypočítať Pytagorovou vetou:

\ [\ begin (zarovnanie) & \ vľavo | ((v) _ (1)) \ vpravo | = \ sqrt ((((1) ^ (2)) + ((\ left (-1 \ right)) ^ (2))) = \ sqrt (2); \\ & \ vľavo | ((v) _ (2)) \ vpravo | = \ sqrt ((((2) ^ (2)) + ((2) ^ (2))) = \ sqrt (8) = 2 \ sqrt (2); \\ & S = \ vľavo | ((v) _ (1)) \ vpravo | \ cdot \ vľavo | ((v) _ (2)) \ vpravo | = \ sqrt (2) \ cdot 2 \ sqrt (2) = 4. \\\ end (zarovnať) \]

Zostáva sa zaoberať posledným determinantom - už existuje matica 3x3. Musíme si zapamätať stereometriu:

Determinant 3x3 je objem rovnobežnostena

Vyzerá to, že pohlcuje mozog, ale v skutočnosti to stačí na pripomenutie vzorca pre objem rovnobežnostena:

kde $ S $ je plocha základne (v našom prípade je to plocha rovnobežníka v rovine $ OXY $), $ h $ je výška nakreslená k tejto základni (v skutočnosti je $ z $ -súradnica vektora $ ((v) _ (3)) $).

Plochu rovnobežníka (nakreslili sme ho samostatne) je tiež ľahké vypočítať:

\ [\ begin (zarovnanie) & S = 2 \ cdot 3 = 6; \\ & V = S \ cdot h = 6 \ cdot 4 = 24. \\\ end (zarovnať) \]

To je všetko! Odpovede zapisujeme.

Odpoveď: 3; 4; 24.

Krátka poznámka k systému zápisov. Niekomu sa asi nebude páčiť, že ignorujem „šípky“ nad vektormi. Údajne si týmto spôsobom môžete zameniť vektor s bodom alebo niečím iným.

Ale buďme vážni: ty a ja sme už dospelí chlapci a dievčatá, takže z kontextu dokonale chápeme, kedy ide o vektor a kedy o niečo. Šípky len zanášajú príbeh, už napchatý matematickými vzorcami k očným bulvám.

A ďalej. V zásade nám nič nebráni zvážiť determinant matice 1x1 - taká matica je iba jedna bunka a číslo zapísané v tejto bunke bude určujúcim faktorom. Ale je tu dôležitá poznámka:

Na rozdiel od klasického objemu nám determinant poskytne takzvaný „ orientovaný objem", Tj. objem, pričom sa zohľadní postupnosť zvažovania riadkových vektorov.

A ak chcete získať objem v klasickom zmysle slova, musíte použiť determinantový modul, ale teraz by ste si s tým nemali robiť starosti - každopádne sa o niekoľko sekúnd naučíme počítať akýkoľvek determinant s akýmikoľvek znakmi , veľkosti a pod :)

Algebraická definícia

Napriek všetkej kráse a jasnosti geometrického prístupu má vážnu nevýhodu: nehovorí nič o tom, ako počítať tento veľmi rozhodujúci faktor.

Preto teraz budeme analyzovať alternatívnu definíciu - algebraickú. Na to potrebujeme krátku teoretickú prípravu, ale na konci dostaneme nástroj, ktorý nám umožní spočítať čokoľvek v maticiach a ako chceme.

Je pravda, že nastane nový problém ... ale najskôr.

Permutácie a inverzie

Zapíšte si čísla od 1 do $ n $ do riadka. Skončíte s niečím takýmto:

Teraz (čisto zo zábavy) si prehodíme pár čísel. Susedné môžete zmeniť:

Alebo môžete - nie je obzvlášť susedné:

A vieš čo? Ale nič! V algebre sa toto svinstvo nazýva permutácia. A ona má veľa vlastností.

Definícia. Permutácia dĺžky $ n $ je reťazec odlišných čísel $ n $ zapísaných v ľubovoľnom poradí. Obvykle sa berú do úvahy prvé $ n $ prirodzené čísla (to znamená iba čísla 1, 2, ..., $ n $) a potom sa zmiešajú, aby sa získala požadovaná permutácia.

Permutácie sa označujú rovnako ako vektory - iba písmeno a sekvenčný zoznam ich prvkov v zátvorkách. Napríklad: $ p = \ vľavo (1; 3; 2 \ vpravo) $ alebo $ p = \ vľavo (2; 5; 1; 4; 3 \ vpravo) $. Písmeno môže byť čokoľvek, ale nech je to $ p $. :)

Ďalej, kvôli jednoduchosti budeme pracovať s permutáciami dĺžky 5 - sú už dostatočne vážne na to, aby pozorovali akékoľvek podozrivé efekty, ale ešte nie sú také závažné pre nezrelý mozog ako permutácie s dĺžkou 6 a viac. Tu sú príklady takýchto permutácií:

\ [\ begin (align) & ((p) _ (1)) = \ left (1; 2; 3; 4; 5 \ right) \\ & ((p) _ (2)) = \ left (1 ; 3; 2; 5; 4 \ right) \\ & ((p) _ (3)) = \ left (5; 4; 3; 2; 1 \ right) \\\ end (align) \]

Prirodzene, na permutáciu dĺžky $ n $ je možné pozerať ako na funkciu, ktorá je definovaná na množine $ \ left \ (1; 2; ...; n \ right \) $ a túto množinu na seba bijektívne mapuje. Keď sa vrátime k práve napísaným permutáciám $ ((p) _ (1)) $, $ ((p) _ (2)) $ a $ ((p) _ (3)) $, môžeme celkom legálne napísať:

\ [((p) _ (1)) \ vľavo (1 \ vpravo) = 1; ((p) _ (2)) \ vľavo (3 \ vpravo) = 2; ((p) _ (3)) \ vľavo (2 \ vpravo) = 4; \]

Počet rôznych permutácií dĺžky $ n $ je vždy ohraničený a rovný $ n! $ - to je ľahko dokázateľný fakt z kombinatoriky. Ak napríklad chceme zapísať všetky permutácie dĺžky 5, budeme veľmi váhať, pretože takéto permutácie budú existovať.

Jednou z kľúčových charakteristík akejkoľvek permutácie je počet jej inverzií.

Definícia. Inverzia v permutácii $ p = \ left (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \ right) $ - ľubovoľný pár $ \ left (((a) _ (i)); ((a) _ (j)) \ right) $ také, že $ i \ lt j $, ale $ ((a) _ (i)) \ gt (( a) _ (j)) $. Jednoducho povedané, inverzia je, keď je väčšie číslo vľavo od menšieho (nie nevyhnutne susedného).

Budeme označovať $ N \ left (p \ right) $ počet inverzií v permutácii $ p $, ale buďte pripravení stretnúť sa s inými označeniami v rôznych učebniciach a rôznymi autormi - neexistujú tu jednotné štandardy. Téma inverzií je pomerne rozsiahla a bude jej venovaná samostatná lekcia. Teraz je našou úlohou jednoducho naučiť sa ich počítať v skutočných problémoch.

Počítajme napríklad počet inverzií v permutácii $ p = \ left (1; 4; 5; 3; 2 \ right) $:

\ [\ left (4; 3 \ right); \ left (4; 2 \ right); \ left (5; 3 \ right); \ left (5; 2 \ right); \ left (3; 2 \ right ). \]

Takže $ N \ vľavo (p \ vpravo) = 5 $. Ako vidíte, nie je na tom nič zlé. Poviem vám to hneď: ďalej nás nebude zaujímať ani tak samotný počet $ N \ left (p \ right) $, ako jeho rovnomernosť / zvláštnosť. A tu plynule prechádzame ku kľúčovému termínu dnešnej hodiny.

Čo je determinant

Nech je zadaná štvorcová matica $ A = \ left [n \ times n \ right] $. Potom:

Definícia. Determinant matice $ A = \ left [n \ times n \ right] $ je algebraický súčet podmienok $ n! $, Zostavených nasledovne. Každý výraz je súčinom prvkov matice $ n $, odobratých po jednom z každého riadka a každého stĺpca, vynásobeného (−1) mocninou počtu inverzií:

\ [\ vľavo | A \ right | = \ suma \ limity_ (n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

Základným bodom pri výbere faktorov pre každý výraz v determinante je skutočnosť, že žiadne dva faktory nie sú v rovnakom riadku alebo v tom istom stĺpci.

Vzhľadom na to môžeme bez straty všeobecnosti predpokladať, že indexy $ i $ faktorov $ ((a) _ (i; j)) $ „prechádzajú“ hodnotami 1, ..., $ n $ , a indexy $ j $ sú určitou permutáciou prvého:

A keď dôjde k permutácii $ p $, môžeme ľahko vypočítať inverzie $ N \ left (p \ right) $ - a ďalší termín determinantu je pripravený.

Prirodzene, nikto nezakazuje výmenu multiplikátorov v akomkoľvek termíne (alebo vo všetkých naraz - prečo strácať čas drobnosťami?), A potom prvé indexy budú tiež predstavovať určitú permutáciu. Nakoniec sa však nič nezmení: celkový počet inverzií v indexoch $ i $ a $ j $ si pri týchto zvrátenostiach zachováva paritu, čo je celkom v súlade so starým dobrým pravidlom:

Preskupenie faktorov nemení súčin čísel.

Neviažte toto pravidlo na maticové násobenie - na rozdiel od násobenia čísel nie je komutatívne. Ale odbočujem. :)

Matica 2x2

V skutočnosti môžete zvážiť maticu 1x1 - bude to jedna bunka a jej determinant, ako by ste mohli hádať, sa rovná číslu napísanému v tejto bunke. Nič zaujímavé.

Uvažujme teda o štvorcovej matici 2x2:

\ [\ left [\ begin (matica) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ koniec (matica) \ vpravo] \]

Pretože počet riadkov v ňom je $ n = 2 $, determinant bude obsahovať výrazy $ n! = 2! = 1 \ cdot 2 = 2 $. Vypíšeme ich:

\ [\ begin (zarovnanie) & ((\ left (-1 \ right)) ^ (N \ left (1; 2 \ right))) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((\ left (-1 \ right)) ^ (0)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((a) _ (11)) (a) _ (22)); \\ & ((\ left (-1 \ right)) ^ (N \ left (2; 1 \ right))) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((\ left (-1 \ right)) ^ (1)) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((a) _ (12)) ( a) _ (21)). \\\ end (zarovnať) \]

Očividne neexistujú žiadne inverzie v permutácii $ \ left (1; 2 \ right) $, ktorá pozostáva z dvoch prvkov, takže $ N \ left (1; 2 \ right) = 0 $. Ale v permutácii $ \ left (2; 1 \ right) $ je jedna inverzia (v skutočnosti 2< 1), поэтому $N\left(2;1 \right)=1.$

Univerzálny vzorec na výpočet determinantu pre maticu 2x2 vyzerá celkom takto:

\ [\ vľavo | \ begin (matica) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ end ( matica) \ vpravo | = ((a) _ (11)) ((a) _ (22)) - ((a) _ (12)) ((a) _ (21)) \]

Graficky to môže byť reprezentované ako súčin prvkov na hlavnej uhlopriečke mínus súčin prvkov na bočnej:

Determinant matice 2x2

Pozrime sa na niekoľko príkladov:

\ [\ vľavo | \ begin (matica) 5 & 6 \\ 8 & 9 \\\ end (matica) \ right |; \ quad \ left | \ begin (matica) 7 & 12 \\ 14 & 1 \\\ end (matica) \ right |. \]

Riešenie. Všetko sa počíta v jednom riadku. Prvá matica:

A ten druhý:

Odpoveď: −3; −161.

Bolo to však príliš jednoduché. Pozrime sa na matice 3x3 - tam je to už zaujímavé.

Matica 3x3

Teraz zvážte štvorcovú maticu 3x3:

\ [\ left [\ begin (matica) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & (a) _ (22)) & (a) _ (23)) \\ ((a) _ (31)) & (a) _ (32)) & (a) _ (33) ) \\\ end (matica) \ right] \]

Pri výpočte jeho determinantu dostaneme 3 doláre! = 1 \ cdot 2 \ cdot 3 = 6 $ výrazov - nie príliš na paniku, ale dosť na to, aby ste začali hľadať nejaké vzorce. Najprv napíšeme všetky permutácie troch prvkov a vypočítame inverzie v každom z nich:

\ [\ begin (align) & ((p) _ (1)) = \ left (1; 2; 3 \ right) \ Rightarrow N \ left ((((p) _ (1)) \ right) = N \ vľavo (1; 2; 3 \ vpravo) = 0; \\ & ((p) _ (2)) = \ left (1; 3; 2 \ right) \ Rightarrow N \ left ((((p) _ (2)) \ right) = N \ left (1; 3 ; 2 \ vpravo) = 1; \\ & ((p) _ (3)) = \ left (2; 1; 3 \ right) \ Rightarrow N \ left ((((p) _ (3)) \ right) = N \ left (2; 1 ; 3 \ vpravo) = 1; \\ & ((p) _ (4)) = \ left (2; 3; 1 \ right) \ Rightarrow N \ left ((((p) _ (4)) \ right) = N \ left (2; 3 ; 1 \ vpravo) = 2; \\ & ((p) _ (5)) = \ left (3; 1; 2 \ right) \ Rightarrow N \ left ((((p) _ (5)) \ right) = N \ left (3; 1 ; 2 \ vpravo) = 2; \\ & ((p) _ (6)) = \ left (3; 2; 1 \ right) \ Rightarrow N \ left ((((p) _ (6)) \ right) = N \ left (3; 2 ; 1 \ vpravo) = 3. \\\ end (zarovnať) \]

Podľa očakávania bolo zmenených celkom 6 permutácií $ ((p) _ (1)) $, ... $ ((p) _ (6)) $) a počet inverzií v nich sa mení od 0 do 3.

Vo všeobecnosti budeme mať tri výrazy s „plus“ (kde $ N \ vľavo (p \ vpravo) $ je párne) a tri ďalšie s „mínus“. Determinant sa vo všeobecnosti vypočíta podľa vzorca:

\ [\ vľavo | \ begin (matica) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & (a) _ (23)) \\ ((a) _ (31)) & (a) _ (32)) & (a) _ (33)) \\\ koniec (matica) \ vpravo | = \ začiatok (matica) ((a) _ (11)) ((a) _ (22)) ((a) _ (33)) + ((a) _ (12)) ( a) _ (23)) (a) _ (31)) + (a) _ (13)) (a) _ (21)) (a) _ (32)) - \\ - ( a) _ (13)) (a) _ (22)) (a) _ (31)) - (a) _ (12)) (a) _ (21)) ((a) _ (33)) - ((a) _ (11)) (a) _ (23)) ((a) _ (32)) \\\ koniec (matica) \]

Len si teraz nesadajte a zúrivo napchávajte všetky tieto indexy! Namiesto nezrozumiteľných čísel je lepšie pamätať na nasledujúce mnemotechnické pravidlo:

Pravidlo trojuholníka. Ak chcete nájsť determinant matice 3x3, musíte pridať tri produkty prvkov na hlavnú uhlopriečku a na vrcholy rovnoramenných trojuholníkov so stranou rovnobežnou s touto uhlopriečkou a potom odpočítať tri rovnaké produkty, ale na bočnej uhlopriečke. Schematicky to vyzerá takto:

Determinant matice 3x3: pravidlo trojuholníka

Práve tieto trojuholníky (alebo pentagramy - ako sa vám páči) radi kreslia do všetkých druhov učebníc a príručiek o algebre. Nehovorme však o smutných veciach. Poďme si lepšie vypočítať jeden taký determinant - na zahriatie pred skutočným cínom. :)

Úloha. Vypočítajte determinant:

\ [\ vľavo | \ begin (matrix) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\ end (matrix) \ right | \]

Riešenie. Pracujeme podľa pravidla trojuholníkov. Najprv spočítajme tri výrazy zložené z prvkov na hlavnej diagonále a rovnobežne s ňou:

\ [\ begin (zarovnanie) & 1 \ cdot 5 \ cdot 1 + 2 \ cdot 6 \ cdot 7 + 3 \ cdot 4 \ cdot 8 = \\ & = 5 + 84 + 96 = 185 \\\ end (zarovnanie) \]

Teraz sa zaoberáme bočnou uhlopriečkou:

\ [\ begin (zarovnanie) & 3 \ cdot 5 \ cdot 7 + 2 \ cdot 4 \ cdot 1 + 1 \ cdot 6 \ cdot 8 = \\ & = 105 + 8 + 48 = 161 \\\ end (zarovnanie) \]

Zostáva iba odpočítať druhé od prvého čísla - a dostaneme odpoveď:

To je všetko!

Maticové determinanty 3x3 však ešte nie sú vrcholom zručnosti. To najzaujímavejšie nás čaká ďalej. :)

Všeobecná schéma výpočtu determinantov

Ako vieme, ako rastie rozmer matice $ n $, počet výrazov v determinante je $ n! $ A rýchlo rastie. Koniec koncov, faktoriál nie je pre vás nič zatraceně, skôr rýchlo rastúca funkcia.

Už pre matice 4x4 nie je dobré hodnotiť determinanty priamo vpred (t.j. prostredníctvom permutácií). Asi 5x5 a viac spravidla mlčte. Preto sú niektoré vlastnosti determinantu spojené s prípadom, ale na ich pochopenie je potrebná malá teoretická príprava.

Pripravený? Choď!

Čo je to Matrix Minor

Nech je daná ľubovoľná matica $ A = \ left [m \ times n \ right] $. Poznámka: Nie nevyhnutne štvorcový. Na rozdiel od determinantov sú mladiství také veci, ktoré existujú nielen v drsných štvorcových matriciach. Vyberme niekoľko (napríklad $ k $) riadkov a stĺpcov v tejto matici s $ 1 \ le k \ le m $ a $ 1 \ le k \ le n $. Potom:

Definícia. Menšia hodnota poradia $ k $ je determinantom štvorcovej matice, ktorá vzniká na priesečníku vybratých stĺpcov a riadkov $ k $. Túto novú maticu budeme tiež nazývať menšou.

Takáto maloletá osoba sa označuje ako $ ((M) _ (k)) $. Prirodzene, jedna matica môže mať celú skupinu mladistvých rádovo $ k $. Tu je príklad vedľajšej objednávky 2 pre maticu $ \ left [5 \ times 6 \ right] $:

Výberom $ k = 2 $ stĺpcov a riadkov vytvoríte vedľajšie

Nie je potrebné, aby vybrané riadky a stĺpce boli vedľa seba, ako v príklade vyššie. Hlavná vec je, že počet vybraných riadkov a stĺpcov je rovnaký (toto je číslo $ k $).

Existuje aj ďalšia definícia. Možno sa niekomu bude páčiť viac:

Definícia. Nech je zadaná obdĺžniková matica $ A = \ left [m \ times n \ right] $. Ak sa po odstránení jedného alebo viacerých stĺpcov a jedného alebo niekoľkých riadkov v ňom vytvorí štvorcová matica s veľkosťou $ \ left [k \ times k \ right] $, potom je jej determinantom menšia $ ((M) _ (k) ) $ ... Maticu budeme tiež niekedy nazývať menšou - to bude zrejmé z kontextu.

Ako moja mačka hovorievala, niekedy je lepšie zabaliť sa z 11. poschodia, aby ste jedli jedlo raz, ako mňoukať, keď sedíte na balkóne.

Príklad. Vzhľadom na maticu

Výberom riadka 1 a stĺpca 2 dostaneme menšiu objednávku prvého poriadku:

\ [((M) _ (1)) = \ vľavo | 7 \ vpravo | = 7 \]

Výberom riadkov 2, 3 a stĺpcov 3, 4 dostaneme menšiu časť druhého poriadku:

\ [((M) _ (2)) = \ vľavo | \ begin (matica) 5 & 3 \\ 6 & 1 \\\ end (matica) \ right | = 5-18 = -13 \]

A ak vyberiete všetky tri riadky, ako aj stĺpce 1, 2, 4, bude existovať vedľajší príkaz tretieho rádu:

\ [((M) _ (3)) = \ vľavo | \ begin (matica) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\ end (matica) \ right | \]

Pre čitateľa nebude ťažké nájsť ďalších neplnoletých rádov 1, 2 alebo 3. Preto poďme ďalej.

Algebraické doplnky

„Dobre, a čo nám títo prisluhovači dajú?“ - pravdepodobne sa pýtaš. Sami, nič. Ale v štvorcových matriciach má každý menší „spoločníka“ - dodatočného neplnoletého a tiež algebraický doplnok. A spoločne nám tieto dva triky umožnia kliknúť na kvalifikácie ako orechové.

Definícia. Nech je daná štvorcová matica $ A = \ left [n \ times n \ right] $, v ktorej je vybraté vedľajšie $ ((M) _ (k)) $. Potom je dodatočná menšia skupina pre vedľajšiu skupinu $ ((M) _ (k)) $ časťou pôvodnej matice $ A $, ktorá zostane po vymazaní všetkých riadkov a stĺpcov, ktoré sa podieľajú na zostavení vedľajšej hodnoty $ ((M) _ ( k)) $:

Dodatočné menšie až menšie $ ((M) _ (2)) $

Ujasnime si jeden bod: dodatočná maloletá osoba nie je len „kúskom matice“, ale determinantom tejto časti.

Ďalší neplnoletí sú označení hviezdičkou: $ M_ (k) ^ (*) $:

kde operácia $ A \ nabla ((M) _ (k)) $ doslova znamená „odstrániť z $ A $ riadky a stĺpce zahrnuté v $ ((M) _ (k)) $“. Táto operácia nie je v matematike všeobecne akceptovaná - práve som ju vymyslel pre krásu príbehu. :)

Doplnkové maloleté osoby sa len zriedka používajú samy. Sú súčasťou komplexnejšej konštrukcie, algebraického doplnku.

Definícia. Vedľajší doplnok $ ((M) _ (k)) $ je dodatočný menší $ M_ (k) ^ (*) $ vynásobený $ ((\ left (-1 \ right)) ^ (S)) $, kde $ S $ je súčet čísel všetkých riadkov a stĺpcov zahrnutých v pôvodnom minoritnom $ ((M) _ (k)) $.

Algebraický doplnok vedľajšej $ ((M) _ (k)) $ je spravidla označený $ ((A) _ (k)) $. Preto:

\ [((A) _ (k)) = ((\ \ left (-1 \ right)) ^ (S)) \ cdot M_ (k) ^ (*) \]

Ťažko? Na prvý pohľad áno. Ale nie je to úplne tak. Pretože v skutočnosti je všetko jednoduché. Uvažujme o príklade:

Príklad. Vzhľadom na maticu 4x4:

Vyberme menšiu osobu druhého rádu

\ [((M) _ (2)) = \ vľavo | \ begin (matrix) 3 & 4 \\ 15 & 16 \\\ end (matrix) \ right | \]

Kapitán Obivid nám akosi naznačuje, že pri skladaní tejto molly boli zahrnuté riadky 1 a 4, ako aj stĺpce 3 a 4. Prečiarknite ich - získame ďalšiu maloletú:

Zostáva nájsť číslo $ S $ a získať algebraický doplnok. Pretože poznáme čísla príslušných riadkov (1 a 4) a stĺpcov (3 a 4), je všetko jednoduché:

\ [\ begin (zarovnanie) & S = 1 + 4 + 3 + 4 = 12; \\ & ((A) _ (2)) = ((\ \ left (-1 \ right)) ^ (S)) \ cdot M_ (2) ^ (*) = ((\ left (-1 \ right) ) ^ (12)) \ cdot \ left (-4 \ right) = - 4 \ end (align) \]

Odpoveď: $ ((A) _ (2)) = - 4 $

To je všetko! V skutočnosti je všetok rozdiel medzi dodatočným menším a algebraickým doplnkom iba v mínuse vpredu a dokonca aj vtedy nie vždy.

Laplaceova veta

A tak sme prišli na to, prečo sú v skutočnosti všetky tieto mladistvé a algebraické doplnky potrebné.

Laplaceova veta o rozšírení determinantu. Nechajte riadky (stĺpce) $ k $ vybrať v matici veľkosti $ \ left [n \ times n \ right] $, pričom $ 1 \ le k \ le n-1 $. Potom je determinant tejto matice rovný súčtu všetkých produktov mladistvých rádu $ k $ obsiahnutých vo vybraných riadkoch (stĺpcoch) ich algebraickými doplnkami:

\ [\ vľavo | A \ right | = \ sum ((((M) _ (k)) \ cdot ((A) _ (k))) \]

Okrem toho budú existovať presne tieto výrazy $ C_ (n) ^ (k) $.

Dobre, dobre: ​​asi $ C_ (n) ^ (k) $ - Už o tom hovorím, v pôvodnej Laplaceovej vete nič také nebolo. Nikto však nezrušil kombinatoriku a doslova zbežný pohľad na stav vám umožní ubezpečiť sa, že výrazov bude presne toľko. :)

Nebudeme to dokazovať, aj keď to nepredstavuje žiadne zvláštne ťažkosti - všetky výpočty sú redukované na staré dobré permutácie a párne / nepárne inverzie. Napriek tomu bude dôkaz predložený v samostatnom odseku a dnes tu máme čisto praktickú lekciu.

Preto prechádzame na špeciálny prípad tejto vety, keď sú mladistvými oddelené bunky matice.

Determinantný rozklad podľa riadka a stĺpca

To, o čom sa teraz bude diskutovať, je presne hlavným nástrojom práce s determinantmi, kvôli ktorému sa začala celá táto hra s permutáciami, mladistvými a algebraickými doplnkami.

Čítajte a užívajte si:

Dôsledok z Laplaceovej vety (rozšírenie riadka / stĺpca determinantu). Nechajte vybrať jeden riadok v matici veľkosti $ \ left [n \ times n \ right] $. Maloletými v tomto riadku budú $ n $ jednotlivé bunky:

\ [((M) _ (1)) = ((a) _ (ij)), \ quad j = 1, ..., n \]

Vypočítať sa dajú aj ďalšie neplnoleté osoby: vezmite pôvodnú maticu a odstráňte riadok a stĺpec obsahujúci $ ((a) _ (ij)) $. Nazvime takých mladistvých $ M_ (ij) ^ (*) $.

Pre algebraický doplnok je tiež potrebné číslo $ S $, ale v prípade menšej hodnoty rádu 1 je to len súčet „súradníc“ bunky $ ((a) _ (ij)) $:

A potom môže byť pôvodný determinant zapísaný v zmysle $ ((a) _ (ij)) $ a $ M_ (ij) ^ (*) $ podľa Laplaceovej vety:

\ [\ vľavo | A \ right | = \ sum \ limits_ (j = 1) ^ (n) ((((a) _ (ij)) \ cdot ((\ left (-1 \ right)) ^ (i + j)) \ cdot ((M) _ (ij))) \]

Tak to je vzorec rozšírenia reťazca... To isté však platí pre stĺpce.

Z tohto dôsledku je možné vyvodiť niekoľko záverov:

1. Táto schéma funguje rovnako dobre pre riadky aj stĺpce. V skutočnosti bude rozšírenie častejšie nie po riadkoch, ale po stĺpcoch.
2. Počet výrazov v rozšírení je vždy presne $ n $. To je výrazne menej ako $ C_ (n) ^ (k) $ a ešte viac $ n! $.
3. Namiesto jedného determinantu $ \ left [n \ times n \ right] $ budete musieť počítať niekoľko determinantov veľkosti o jednu menej: $ \ left [\ left (n-1 \ right) \ times \ left (n-1 \ right) \ right] $.

Posledná skutočnosť je obzvlášť dôležitá. Napríklad namiesto brutálneho determinantu 4x4 bude teraz stačiť spočítať niekoľko determinantov 3x3 - nejako sa s nimi vysporiadame. :)

Úloha. Nájdite determinant:

\ [\ vľavo | \ begin (matrix) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\ end (matrix) \ right | \]

Riešenie. Rozviňme tento determinant v prvom riadku:

\ [\ begin (zarovnanie) \ vľavo | A \ right | = 1 \ cdot ((\ \ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (matica) 5 & 6 \\ 8 & 9 \\\ end (matica) \ right | + & \\ 2 \ cdot ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ vľavo | \ begin (matica) 4 & 6 \\ 7 & 9 \\\ end (matica) \ right | + & \\ 3 \ cdot ((\ left (-1 \ right)) ^ (1 + 3)) \ cdot \ vľavo | \ begin (matica) 4 & 5 \\ 7 & 8 \\\ end (matica) \ right | = & \\\ end (align) \]

\ [\ begin (zarovnanie) & = 1 \ cdot \ left (45-48 \ right) -2 \ cdot \ left (36-42 \ right) +3 \ cdot \ left (32-35 \ right) = \\ & = 1 \ cdot \ left (-3 \ right) -2 \ cdot \ left (-6 \ right) +3 \ cdot \ left (-3 \ right) = 0. \\\ end (zarovnať) \]

Úloha. Nájdite determinant:

\ [\ vľavo | \ begin (matica) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ end (matica) \ right | \ ]

Riešenie. Pre zmenu tentokrát pracujme so stĺpcami. Napríklad posledný stĺpec obsahuje dve nuly naraz - evidentne to výrazne zníži výpočty. Teraz uvidíte, prečo.

Rozširujeme teda determinant o štvrtý stĺpec:

\ [\ begin (zarovnanie) \ vľavo | \ begin (matica) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ end (matica) \ right | = 0 \ cdot ((\ left (-1 \ right)) ^ (1 + 4)) \ cdot \ left | \ begin (matica) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ end (matica) \ right | + & \\ +1 \ cdot ((\ left (-1 \) vpravo)) ^ (2 + 4)) \ cdot \ vľavo | \ begin (matica) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ end (matica) \ right | + & \\ +1 \ cdot ((\ left (-1 \) vpravo)) ^ (3 + 4)) \ cdot \ vľavo | \ begin (matica) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ end (matica) \ right | + & \\ +0 \ cdot ((\ left (-1 \) vpravo)) ^ (4 + 4)) \ cdot \ vľavo | \ begin (matica) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\ end (matica) \ right | & \\\ end (zarovnať) \]

A potom - oh, zázrak! - dva výrazy okamžite klesnú, pretože majú multiplikátor „0“. Stále existujú dva determinanty 3x3, s ktorými sa môžeme ľahko vysporiadať:

\ [\ begin (zarovnanie) & \ vľavo | \ begin (matica) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ end (matica) \ right | = 0 + 0 + 1-1-1-0 = -1; \\ & \ vľavo | \ begin (matica) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ end (matica) \ right | = 0 + 1 + 1-0-0-1 = 1. \\\ end (zarovnať) \]

Vrátime sa k zdroju a nájdeme odpoveď:

\ [\ vľavo | \ begin (matica) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ end (matica) \ right | = 1 \ cdot \ left (-1 \ right) + \ left (-1 \ right) \ cdot 1 = -2 \]

To je teda všetko. A nie 4! = 24 termínov nebolo potrebné započítať. :)

Odpoveď: -2

Základné vlastnosti determinantu

V poslednom probléme sme videli, ako prítomnosť núl v riadkoch (stĺpcoch) matice výrazne zjednodušuje expanziu determinantu a všeobecne všetky výpočty. Vyvstáva prirodzená otázka: je možné dosiahnuť, aby sa tieto nuly objavili aj v matici, kde pôvodne neboli?

Odpoveď je jednoznačná: môcť... A tu nám pomáhajú vlastnosti determinantu:

1. Ak prehodíte na miesto dva riadky (stĺpce), determinant sa nezmení;
2. Ak sa jeden riadok (stĺpec) vynásobí číslom $ k $, potom sa celý determinant vynásobí aj číslom $ k $;
3. Ak vezmete jeden riadok a pridáte ho (odčítate) toľkokrát, koľkokrát chcete, od iného, ​​determinant sa nezmení;
4. Ak sú dva riadky determinantu rovnaké, buď proporcionálne, alebo je jeden z riadkov vyplnený nulami, potom je celý determinant nulový;
5. Všetky vyššie uvedené vlastnosti platia aj pre stĺpce.
6. Keď je matica transponovaná, determinant sa nemení;
7. Determinant maticového produktu sa rovná súčinu determinantov.

Tretia vlastnosť má osobitnú hodnotu: môžeme odčítajte ďalší z jedného riadka (stĺpca), kým sa na správnych miestach nezobrazia nuly.

Výpočty sa najčastejšie obmedzujú na „vynulovanie“ celého stĺpca všade, s výnimkou jedného prvku, a potom rozšírenie determinantu pozdĺž tohto stĺpca, čím sa získa matica o 1 menšiu veľkosť.

Pozrime sa, ako to funguje v praxi:

Úloha. Nájdite determinant:

\ [\ vľavo | \ begin (matrix) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ end (matrix) \ right | \ ]

Riešenie. Tu vôbec nie sú žiadne nuly, takže môžete „kladivom“ v ľubovoľnom riadku alebo stĺpci - množstvo výpočtov bude približne rovnaké. Nestrácajme čas drobnosťami a „vynulovaním“ prvého stĺpca: už má bunku s jednou, takže stačí vziať prvý riadok a odpočítať ho 4 -krát od druhého, 3 -krát od tretieho a 2 -krát od posledného.

V dôsledku toho dostaneme novú maticu, ale jej determinant bude rovnaký:

\ [\ begin (matica) \ vľavo | \ begin (matrix) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ end (matrix) \ right | \ begin (matrix) \ downarrow \\ -4 \\ -3 \\ -2 \\\ end (matrix) = \\ = \ left | \ begin (matica) 1 & 2 & 3 & 4 \\ 4-4 \ cdot 1 & 1-4 \ cdot 2 & 2-4 \ cdot 3 & 3-4 \ cdot 4 \\ 3-3 \ cdot 1 & 4-3 \ cdot 2 & 1-3 \ cdot 3 & 2-3 \ cdot 4 \\ 2-2 \ cdot 1 & 3-2 \ cdot 2 & 4-2 \ cdot 3 & 1-2 \ cdot 4 \ \\ koniec (matica) \ vpravo | = \\ = \ vľavo | \ begin (matica) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \ koniec (matica) \ vpravo | \\\ koniec (matica) \]

Teraz, s prasiatkovou vyrovnanosťou, rozšírime tento determinant podľa prvého stĺpca:

\ [\ begin (matica) 1 \ cdot ((\ \ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (matica) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ end (matica) \ right | +0 \ cdot ((\ vľavo (-1 \ vpravo)) ^ (2 + 1)) \ cdot \ vľavo | ... \ \ right | + \\ +0 \ cdot ((\ \ left (-1 \ right)) ^ (3 + 1)) \ cdot \ left | ... \ \ right | +0 \ cdot ((\ \ left (-1 \ right)) ^ (4 + 1)) \ cdot \ left | ... \ vpravo | \\\ koniec (matica) \]

Je jasné, že „prežije“ iba prvý výraz - vo zvyšku som determinanty ani nevypísal, pretože aj tak sú vynásobené nulou. Koeficient pred determinantom je rovný jednej, t.j. nemusíš to písať.

„Mínusy“ však môžete odstrániť zo všetkých troch riadkov determinantu. V skutočnosti sme faktor (−1) trikrát presunuli:

\ [\ vľavo | \ begin (matica) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ end (matica) \ right | = \ cdot \ left | \ begin (matica) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ end (matica) \ right | \]

Získali sme malý determinant 3x3, ktorý sa už dá vypočítať pomocou pravidla trojuholníkov. Skúsime to však rozložiť podľa prvého stĺpca - našťastie posledný riadok jeden hrdo obsahuje:

\ [\ begin (zarovnanie) & \ left (-1 \ right) \ cdot \ left | \ begin (matrix) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ end (matrix) \ right | \ begin (matrix) -7 \\ -2 \\ \ uparrow \ \\ koniec (matica) = \ vľavo (-1 \ vpravo) \ cdot \ vľavo | \ begin (matica) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\\ end (matica) \ right | = \\ & = \ cdot \ left | \ begin (matica) -4 & -36 \\ 4 & -4 \\\ end (matica) \ right | = \ left (-1 \ right) \ cdot \ left | \ begin (matica) -4 & -36 \\ 4 & -4 \\\ end (matica) \ right | \\\ end (zarovnať) \]

Môžete si samozrejme zahrať viac zábavy a rozšíriť maticu 2x2 v rade (stĺpci), ale sme adekvátni, takže odpoveď iba vypočítame:

\ [\ vľavo (-1 \ vpravo) \ cdot \ vľavo | \ begin (matica) -4 & -36 \\ 4 & -4 \\\ end (matica) \ right | = \ left (-1 \ right) \ cdot \ left (16 + 144 \ right) = -160 \ ]

Takto sa rozbíjajú sny. Odpoveď iba -160. :)

Odpoveď: -160.

Niekoľko poznámok pred prechodom na poslednú úlohu:

1. Pôvodná matica bola symetrická okolo bočnej uhlopriečky. Všetky mladistvé v expanzii sú tiež symetrické vzhľadom na rovnakú bočnú uhlopriečku.
2. Presne povedané, nemohli sme rozložiť vôbec nič, ale jednoducho priviesť maticu do hornej trojuholníkovej formy, keď sú pod hlavnou uhlopriečkou pevné nuly. Potom (mimochodom, presne v súlade s geometrickou interpretáciou) je determinant rovný súčinu $ ((a) _ (ii)) $ - čísel na hlavnej uhlopriečke.

Úloha. Nájdite determinant:

\ [\ vľavo | \ begin (matrix) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ end (matrix) \ right | \ ]

Riešenie. Tu prvý riadok prosí o „vynulovanie“. Vezmeme prvý stĺpec a odčítame presne raz od všetkých ostatných:

\ [\ begin (zarovnanie) & \ vľavo | \ begin (matrix) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ end (matrix) \ right | = \\ & = \ vľavo | \ begin (matica) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & ​​25-5 & 125-5 & 625-5 \\\ koniec (matica) \ vpravo | = \\ & = \ vľavo | \ begin (matrix) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\ end (matrix) \ right | \\\ end (zarovnať) \]

Rozbalíme v prvom riadku a potom odstránime spoločné faktory zo zvyšných riadkov:

\ [\ cdot \ vľavo | \ begin (matica) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\ end (matica) \ right | = \ cdot \ left | \ begin (matica) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ end (matica) \ right | \]

Opäť pozorujeme „krásne“ čísla, ale už v prvom stĺpci - podľa neho rozširujeme determinant:

\ [\ begin (zarovnanie) & 240 \ cdot \ vľavo | \ begin (matrix) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ end (matrix) \ right | \ begin (matrix) \ downarrow \\ -1 \\ -1 \ \\ koniec (matica) = 240 \ cdot \ vľavo | \ begin (matica) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\ end (matica) \ right | = \\ & = 240 \ cdot ((\ left (-1 \) vpravo)) ^ (1 + 1)) \ cdot \ vľavo | \ begin (matica) 1 & 6 \\ 3 & 24 \\\ end (matica) \ right | = \\ & = 240 \ cdot 1 \ cdot \ left (24-18 \ right) = 1440 \\\ end ( zarovnať) \]

Objednať. Problém je vyriešený.

Odpoveď: 1440

Výpočet determinantov n-tretia objednávka:

Determinantný koncept n-rád

Použitím tohto článku o determinantoch sa určite naučíte, ako riešiť problémy, ako sú tieto:

Vyriešte rovnicu:

a mnoho ďalších, ktoré učitelia radi vymýšľajú.

Determinant matice alebo jednoducho determinant hrá dôležitú úlohu pri riešení systémov lineárnych rovníc. Na tento účel boli vo všeobecnosti vynájdené determinanty. Pretože sa často hovorí aj o „determinante matice“, uvádzame tu aj matice. Matica je obdĺžniková tabuľka tvorená číslami, ktoré nemožno zamieňať. Štvorcová matica je tabuľka, v ktorej je počet riadkov a počet stĺpcov rovnaký. Len štvorcová matica môže mať determinant.

Logiku zápisu determinantov podľa nasledujúceho diagramu je ľahké pochopiť. Zoberme si systém dvoch rovníc s dvoma neznámymi, ktoré sú vám známe zo školy:

V determinante sú koeficienty pre neznáme zapísané postupne: v prvom riadku - z prvej rovnice, v druhom riadku - z druhej rovnice:

Napríklad vzhľadom na sústavu rovníc

potom sa z koeficientov s neznámymi vytvorí nasledujúci determinant:

Dostaňme teda štvorcovú tabuľku pozostávajúcu z čísel nachádzajúcich sa v nčiary (horizontálne rady) a v n stĺpce (zvislé rady). Pomocou týchto čísel sa podľa niektorých pravidiel, ktoré budeme študovať nižšie, nájde číslo, ktoré sa nazýva determinant n-th -order a sú označené nasledovne:

(1)

Čísla sa volajú prvky determinant (1) (prvý index označuje číslo riadku, druhý označuje číslo stĺpca, v priesečníku ktorého sa prvok nachádza; i = 1, 2, ..., n; j= 1, 2, ..., n). Poradie kvalifikátora je počet jeho riadkov a stĺpcov.

Pomyselná čiara spájajúca prvky determinantu, pre ktoré sú oba indexy rovnaké, t.j. prvky

zavolal hlavná uhlopriečka, druhá uhlopriečka je kolaterál.

Výpočet determinantov druhého a tretieho rádu

Ukážme, ako sa vypočítavajú determinanty prvých troch rádov.

Determinantom prvého rádu je samotný prvok, t.j.

Determinant druhého rádu je číslo získané nasledovne:

, (2)

Súčin prvkov na hlavnej a bočných uhlopriečkach.

Rovnosť (2) ukazuje, že súčin prvkov hlavnej uhlopriečky je braný s vlastným znakom a súčin prvkov vedľajšej uhlopriečky s opačným znamienkom .

Príklad 1. Vypočítajte determinanty druhého rádu:

Riešenie. Podľa vzorca (2) nájdeme:

Determinant tretieho rádu je číslo získané nasledovne:

(3)

Tento vzorec je ťažké si zapamätať. Existuje však jednoduché pravidlo tzv pravidlo trojuholníkov , čo uľahčuje reprodukciu výrazu (3). Body, ktoré určujú prvky determinantu, spájame pomocou čiarových segmentov tie z nich, ktoré poskytujú súčin prvkov prvkov determinantu (obr. 1).

Vzorec (3) ukazuje, že produkty prvkov hlavnej uhlopriečky, ako aj prvkov nachádzajúcich sa na vrcholoch dvoch trojuholníkov, ktorých základy sú s ňou rovnobežné, sa berú so svojimi znakmi; s opakom - produkty prvkov bočnej uhlopriečky, ako aj prvky umiestnené na vrcholoch dvoch trojuholníkov, ktoré sú k nej rovnobežné .

Na obr. 1 sú hlavná uhlopriečka a zodpovedajúce základy trojuholníkov a sekundárne uhlopriečky a zodpovedajúce základne trojuholníkov zvýraznené červenou farbou.

Pri výpočte determinantov je veľmi dôležité, rovnako ako na strednej škole, pamätať na to, že číslo so znamienkom mínus vynásobené číslom so znamienkom mínus má za následok číslo so znamienkom plus a číslo so znamienkom plus vynásobené a. číslo so znamienkom mínus ako výsledok dáva číslo so znamienkom mínus.

Príklad 2. Vypočítajte determinant tretieho rádu:

Riešenie. Pomocou pravidla trojuholníkov dostaneme

Výpočet determinantov n-tretia objednávka

Rozklad determinantu podľa riadka alebo stĺpca

Na výpočet determinantu n poradí, je potrebné poznať a používať nasledujúcu vetu.

Laplaceova veta. Determinant sa rovná súčtu súčinov prvkov radu podľa ich algebraických doplnkov, t.j.

Definícia... Ak v determinante n-rozkaz zvoliť si svojvoľne p linky a p stĺpce ( p < n), potom prvky na priesečníku týchto riadkov a stĺpcov tvoria maticu poradia.

Determinant tejto matice sa nazýva vedľajšia pôvodný determinant. Zoberme si napríklad determinant:

Zostavte maticu z riadkov a stĺpcov s párnymi číslami:

Determinant

zavolal vedľajšia determinant. Prijatá menšia osoba druhého rádu. Je zrejmé, že z nich možno skonštruovať rôznych mladistvých prvého, druhého a tretieho rádu.

Ak vezmeme prvok a prečiarkneme riadok a stĺpec v determinante, na ktorého priesečníku stojí, potom dostaneme moll, nazývaný molál prvku, ktorý označíme:

.

Ak sa minoritka vynásobí, kde 3 + 2 je súčet čísel riadkov a stĺpcov, na priesečníku ktorých je prvok, potom sa výsledný súčin nazýva algebraický doplnok prvok a je označený,

Vo všeobecnosti bude menšia časť prvku a algebraický doplnok,

(4)

Napríklad vypočítame algebraické doplnky prvkov a determinant tretieho rádu:

Podľa vzorca (4) dostaneme

Pri rozklade determinantu sa často používa nasledujúca vlastnosť determinantu n-tretia objednávka:

ak k prvkom ktoréhokoľvek riadka alebo stĺpca pripočítame súčin zodpovedajúcich prvkov iného riadka alebo stĺpca konštantným faktorom, potom sa hodnota determinantu nezmení.

Príklad 4.

Najprv odčítajte z prvého a tretieho riadku prvky štvrtého riadku, potom budeme mať

Štvrtý stĺpec získaného determinantu obsahuje tri prvky - nuly. Preto je výhodnejšie rozšíriť tento determinant o prvky štvrtého stĺpca, pretože prvé tri produkty budú nuly. Preto

Riešenie môžete skontrolovať pomocou online determinanty kalkulačky .

A nasledujúci príklad ukazuje, ako je možné výpočet determinantu akéhokoľvek (v tomto prípade štvrtého) poriadku zredukovať na výpočet determinantu druhého rádu.

Príklad 5. Vypočítajte determinant:

Odpočítajme prvky prvého riadku od tretieho riadku a pridáme prvky prvého riadka k prvkom štvrtého riadku, potom budeme mať

V prvom stĺpci sú všetky prvky okrem prvého nuly. To znamená, že determinant môže byť už rozšírený v prvom stĺpci. Ale skutočne nechceme počítať determinant tretieho rádu. Preto urobíme viac transformácií: k prvkom tretieho riadku pripočítame prvky druhého riadku vynásobené 2 a od prvkov štvrtého riadku odčítame prvky druhého riadku. V dôsledku toho môže byť determinant, ktorý je algebraickým doplnkom, samotný rozložený v prvom stĺpci a budeme musieť iba vypočítať determinant druhého rádu a nenechať sa zmiasť v znakoch:

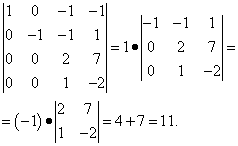
Redukcia determinantu na trojuholníkový tvar

Determinant, kde sú všetky prvky ležiace na jednej strane jednej z uhlopriečok rovné nule, sa nazýva trojuholníkový. Prípad bočnej uhlopriečky sa zmenší na prípad hlavnej uhlopriečky obrátením poradia riadkov alebo stĺpcov. Tento determinant sa rovná súčinu prvkov hlavnej uhlopriečky.

Na prevod do trojuholníkového tvaru sa používa rovnaká vlastnosť determinantu n-tého poriadku, ktorý sme použili v predchádzajúcom odseku: ak súčin zodpovedajúcich prvkov iného riadka alebo stĺpca pripočítame konštantným faktorom k prvkom akéhokoľvek riadka alebo stĺpca, potom sa hodnota determinantu nezmení.

Riešenie môžete skontrolovať pomocou online determinanty kalkulačky .

Determinantné vlastnosti n-rád

V dvoch predchádzajúcich odsekoch sme už použili jednu z vlastností determinantu n tá objednávka. V niektorých prípadoch môžete na zjednodušenie výpočtu determinantu použiť ďalšie dôležité vlastnosti determinantu. Napríklad je možné redukovať determinant na súčet dvoch determinantov, z ktorých jeden alebo obidva je možné pohodlne rozložiť do ľubovoľného riadka alebo stĺpca. Existuje mnoho prípadov takéhoto zjednodušenia a je potrebné rozhodnúť o použití jednej alebo druhej vlastnosti determinantu jednotlivo.

Štvorcová matica A objednať n môže zodpovedať číslu det A(alebo | A|, alebo), nazval to determinant , a to nasledujúcim spôsobom:

Determinant matice A zavolaj jej aj ty determinant ... Pravidlo pre výpočet determinantu pre maticu poradia N. je dosť ťažké pochopiť a používať. Sú však známe metódy, ktoré umožňujú implementovať výpočet determinantov vyšších rádov na základe determinantov nižších rádov. Jedna z metód je založená na vlastnosti rozšírenia determinantu z hľadiska prvkov určitého radu (vlastnosť 7). Zároveň poznamenávame, že je žiaduce vedieť vypočítať determinanty nízkych rádov (1, 2, 3) podľa definície.

Výpočet determinantu 2. rádu ilustruje diagram:

Príklad 4.1. Nájdite determinanty matíc

Na výpočet determinantu tretieho rádu je vhodné použiť pravidlo trojuholníkov (alebo Sarrus), ktorý možno symbolicky napísať takto:

Príklad 4.2. Vypočítajte determinant matice

det A = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.

Sformulujme základné vlastnosti determinantov, ktoré sú vlastné determinantom všetkých rádov. Niektoré z týchto vlastností vysvetľujeme pomocou determinantov tretieho rádu.

Nehnuteľnosť 1 („Rovnosť riadkov a stĺpcov“). Determinant sa nezmení, ak sú jeho riadky nahradené stĺpcami a naopak. Inými slovami,

V nasledujúcom texte sa budú jednoducho volať riadky a stĺpce riadky determinantu .

Nehnuteľnosť 2 ... Po permutácii dvoch rovnobežných radov sa determinant zmení na znamienko.

Nehnuteľnosť 3 ... Determinant s dvoma rovnakými radmi sa rovná nule.

Nehnuteľnosť 4 ... Spoločný faktor prvkov v ľubovoľnom riadku determinantu je možné odstrániť za znamienko determinantu.

Z vlastností 3 a 4 to vyplýva že ak sú všetky prvky určitého radu úmerné zodpovedajúcim prvkom paralelného radu, potom je takýto determinant rovný nule.

Naozaj,

Nehnuteľnosť 5 ... Ak sú prvky ktoréhokoľvek riadka determinantu súčtom dvoch výrazov, potom môže byť determinant rozložený na súčet dvoch zodpovedajúcich determinantov.

Napríklad,

Nehnuteľnosť 6. („Elementárne transformácie determinantu“). Determinant sa nezmení, ak k prvkom jedného radu pridáme zodpovedajúce prvky rovnobežného radu vynásobené ľubovoľným číslom.

Príklad 4.3... Dokáž to

Riešenie: Skutočne pomocou vlastností 5, 4 a 3 budeme učiť

Ďalšie vlastnosti determinantov súvisia s pojmami vedľajšieho a algebraického komplementu.

Menšia nejaký prvok aij determinant n- th poriadok sa nazýva determinant n- 1. rád, získaný z pôvodného odstránením riadka a stĺpca, v ktorého priesečníku sa nachádza vybraný prvok. Označené mij

Algebraický doplnok element aij determinant sa nazýva jeho menší, braný so znamienkom plus, ak je súčet i + j párne číslo a so znamienkom mínus, ak je táto čiastka nepárna. Označené Aij:

Nehnuteľnosť 7 („Rozklad determinantu z hľadiska prvkov určitého radu“). Determinant sa rovná súčtu súčinov prvkov určitého radu zodpovedajúcimi algebraickými doplnkami.